1. What is Dynamic Programming?
- Dynamic programming solves problems by combining the solutions to subproblems. We typically apply dynamic programming to optimization problems. Such problems can have many possible solutions. Each solutions has a value, and we wish to find a solution with the optimal (maximum or minimum) value.
- A sequence of 4 steps:
- Recursively define the value of an optimal solution
- Compute the value of an optimal solution, typically in a bottom-up fashion
- Construct an optimal solution from computed information
- Dynamic programming and recursive are different:
- Dynamic programming starts at resolving smallest subproblems (base problems). From that, we resolve bigger problems until finding the result for biggest problem. (original problem). (bottom-up)
Example:
Fibonaci number
there are 2 methods to compute the fibonaci number bellow:
 |
| computing fibonaci number between recursive and dynamic programming |
the disadvantage of recursive:
 |
| F[6] computation |
2. Some optimization problems
2.1 Rod cutting
Problem description: how to cut a rod into rods of smaller length in way that maximizes their total value. I buy a long steel rod and cut it into shorter rods to sell.
Give a rod of length n inches and a table of prices pi for i= 1, 2, ..., n, determine the maximum revenue rn obtainable by cutting up the rod and selling the prices. If the price pn for a rod of length n is large enoughm, an optimal solution may require no cutting at all.
| A sample price table for rods. |
example: n = 4
the optimal strategy is part (c) - cutting the rod into 2 pieces of length 2 - which has total value 10.
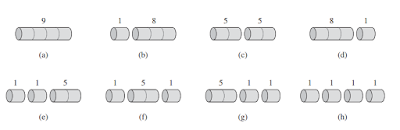 |
| the 8 possible ways of cutting up a rod of length 4 |
If an optimal solution cuts the rod into the k pieces, from some 1 <= k <= n, then an optimal decomposition
n = i1 + i2 + ... + ik;
of the rod ino pieces of lengths i1, i2, i3, .., ik provides maximum corresponding revenue
rn = pi1 + pi2 + .. + pik
 |
| the optimal result |
More generally, we can frame the values rn for n >= 1 in terms of optimal revenues from shorter rods:
the following simpler version of above equation:
 |
| bottom-up dynamic programming version of cut-rod problem |
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
| #include <stdio.h>int main(){ int p[11] = {0, 1, 5, 8, 9, 10, 17, 17, 20, 24, 30}; int r[11]; int s[11]; int i, j; int q; r[0] = 0; for(j = 1; j <= 10; j++) { q = -1; for(i = 1; i <= j; i++) { if(q < p[i] + r[j-i]) { q = p[i] + r[j-i]; s[j] = i; } } r[j] = q; } for(i = 1; i <= 10; i++) printf("r[%d] = %d, s[%d] = %d\n", i, r[i], i, s[i]); return 0;} |
2.2 Matrix-chain multiplication
A1A2A3...An.
so how many are the minimum of scaler multiplications?
matrix-chain multiplication problem:
give a chain <A1, A2, .. An> of n matrices, where i = 1, 2,.., n, matrix Ai has dimension
Step 1:
Call m[i, j] is the optimal value of product Ai...Aj. (i <= j). we must split the product between Ak and Ak+1 for some integer k in range i <= k <=j. That is, for some value of k, we first compute the matrices Ai..k and Ak+1..j and then multiply them together to produce the final product Ai..j. The cost this way is the cost of computing the matrix Ai..j plus the cost pf computing Ak+1...j , plus the cost of multiplying them together.Step 2:
Step 3:
define s[i, j] to be a value of k at which we split the product AiAi+1...Aj in an optimal parenthesization. |
| The algorithm of matrix-chain |
and the below image shows the result of m and s array.
 |
| the m and s tables computed by Matrix-Chain-Order for n = 6 |
The result is ((A1(A2A3))((A4A5)(A6)
the C source code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
| #include <stdio.h>#include <limits.h> // Matrix Ai has dimension p[i-1] x p[i] for i = 1..nint MatrixChainOrder(int p[], int n){ /* For simplicity of the program, one extra row and one extra column are allocated in m[][]. 0th row and 0th column of m[][] are not used */ int m[n][n]; int s[n][n]; int i, j, k, L, q; /* m[i,j] = Minimum number of scalar multiplications needed to compute the matrix A[i]A[i+1]...A[j] = A[i..j] where dimension of A[i] is p[i-1] x p[i] */ // cost is zero when multiplying one matrix. for (i=1; i< n; i++) m[i][i] = 0; // L is chain length. for (L=2; L < n; L++) { for (i=1; i< n-L+1; i++) { j = i+L-1; m[i][j] = INT_MAX; for (k=i; k<= j-1; k++) { // q = cost/scalar multiplications q = m[i][k] + m[k+1][j] + p[i-1]*p[k]*p[j]; if (q < m[i][j]) { m[i][j] = q; s[i][j] = k; } } printf("m[%d][%d] %5d, s[%d][%d] %d \n", i, j, m[i][j], i, j, s[i][j]); } } return m[1][n-1];} int main(){ int i, j; int arr[] = {30, 35, 15, 5, 10, 20, 25}; int arr_size = sizeof(arr)/sizeof(arr[0]); printf("Minimum number of multiplications is %d \n", MatrixChainOrder(arr, arr_size)); return 0;} |




Không có nhận xét nào:
Đăng nhận xét