I: Introduction
Given:
Model this problem with a connected, un-directed graph G = (V, E)
Where:
- V is the set of villages
- E is the set of possible interconnections between pairs of villages.
- (u,v) is a edge ∈ E
- w(u,v) is the cost (amount of wire needed) to connect u and v.
Required:
Find an acyclic subset T ⊆ E that connects all of the node (vertices, villages) and whose total weight
is minimized.
The two algorithm in Section III which are greedy algorithms will find a minimum spanning tree. They do yield a spanning tree with minimum weight.
In this section introduces a "generic" minimum spanning tree method that grows a spanning tree by adding one edge at a time.
The generic method manages a set of edges A, maintaining the following loop variant;
Let G = (V, E) be a connected, undirected graph with a real-valued weight function w defined on E. Let A be a subset of E that is included in some minimum spanning tree for G, let (S, V- S) be any cut of G that respects A, and let (u, v) be a light edge crossing (S, V- S). Then, edge (u, v) is safe for A.
These algorithms use a specific rule to determine a safe edge in line 4 of GENERIC-MST.
Kruskal’s algorithm finds a safe edge to add to the growing forest by finding, of all the edges that connect any two trees in the forest, and edge (u,v) of least weight. Kruskal’s algorithm qualifies as a greedy algorithm because at each step it adds to the forest an edge of least possible weight.
Here is an example of this algorithm
Here is an example code of Kruskal' algorithm
// Code:
// Output:
B: Prim's algorithm
- Since T is acyclic and connects all of the vertices, it must form a tree => Called Spanning Tree.
- The tree T in the required the total weight is minimized named Minimum Spanning Tree.
Figure 1: A minimum spanning tree for a connected graph,
weights on edges, the edges in a minimum spanning tree are shaded.
In Figure 1, the total weight of tree is 37. The minimum spanning tree is not unique: removing the edge (b,c) and replacing it with the edge (a,h) yields another spanning tree with weight 37.
The two algorithm in Section III which are greedy algorithms will find a minimum spanning tree. They do yield a spanning tree with minimum weight.
Applications of minimum spanning tree:
- Civil network planning
- Routing protocols computer networks
- Cluster Analysis
II: Growing a minimum spanning tree
Given:
- A connected, un-directed graph G = (V, E)
- Weight Function w: E -> R
Required:
- Find a minimum spanning tree for G.
Solving problem:
- Prior to each iteration, A is a subset of some minimum spanning tree.
1
2
3
4
5
6
| GENERIC-MST(G,w) A = Ø while A does not form a spanning tree // this means that, all nodes are not connected Find an edge (u, v) that is safe for A A = A ∪ {(u,v)} return A |
Explanation:
- Initialization: After line 2, the set A trivially satisfies the loop invariant.
- Maintenance: The loop in lines 3–5 maintains the invariant by adding only safe edges.
- Termination: All edges added to A are in a minimum spanning tree, and so the set A returned in line 6 must be a minimum spanning tree.
How to determine safe edges by using a rule (which is used in the Section III for two algorithms)
Some definitions:
- A cut (S,V - S) of an undirected graph G = (V, E) is a partition of V. This is illustrated in Figure 2.
- Edge (u,v) ∈ E crosses the cut (S, V - S) if one of its endpoints is in S and the other is in V-S.
- A cut respects a set A of edges if no edge in A crosses the cut .
- An edge is a light edge crossing a cut if its weight is the minimum of any edge crossing the cut.
Figure 2: Two ways of viewing a cut (S, S - V) of the graph from Figure 1
III: The algorithms of Kruskal and Prim
These algorithms use a specific rule to determine a safe edge in line 4 of GENERIC-MST.
A. Kruskal's algorithm
- This algorithm uses disjoint-set data structure to maintain several disjoint sets of elements.
- Each set contains the vertices in one tree of the current forest.
- The operation FIND-SET(u) returns a representative element from the set that contains u (sub-tree that contain u). Thus, we can determine whether two vertices u and v belong to the same tree by testing whether FIND-SET(u) equals FIND-SET(v).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
| MST-KRUSKAL(G,w) A = Ø // Init the set A ti the empty set. for each vertex v ∈ G.V // Create |V| trees (or element), one containing each vertex { MAKE-SET(v) } Sort the edges of G.E into nondecreasing order by weight w // examines edges in order of weight, lowest to highest for each edge (u,v) ∈ G.E, taken in nondecreasing order by weight { if FIND-SET(u) ≠ FIND-SET(v) // whether the endpoints u and v belong the same tree or not (to ensure no circle) { A = A ∪ {(u,v)} // add edge (u,v) to A if it satisfies. UNION(u,v) // merge the vertices of the two trees. } } return A |
Here is an example of this algorithm
Figure 3: The execution of Kruskal’s algorithm on the graph from Figure 1
Here is an example code of Kruskal' algorithm
// Code:
- #include <stdio.h>
- #include <stdlib.h>
- #include <string.h>
- // a structure to represent a weighted edge in graph
- struct Edge
- {
- int src, dest, weight; // source, destination nodes.
- };
- // a structure to represent a connected, undirected and weighted graph
- struct Graph
- {
- // V-> Number of vertices, E-> Number of edges
- int V, E;
- // graph is represented as an array of edges. Since the graph is
- // undirected, the edge from src to dest is also edge from dest
- // to src. Both are counted as 1 edge here.
- struct Edge* edge;
- };
- // Creates a graph with V vertices and E edges
- struct Graph* createGraph(int V, int E)
- {
- struct Graph* graph = (struct Graph*) malloc( sizeof(struct Graph) );
- graph->V = V;
- graph->E = E;
- graph->edge = (struct Edge*) malloc( graph->E * sizeof( struct Edge ) );
- return graph;
- }
- // A structure to represent a subset for union-find
- struct subset
- {
- int *list; // store vaule of vertice which has been unioned into a tree.
- int index; // index for list above or number of elements
- };
- // A utility function to find set of the element i
- int find(struct subset subsets[], int i, int V)
- {
- // find root and make root as parent of i (path compression)
- int subsetIndex;
- for(subsetIndex = 0; subsetIndex < V; subsetIndex++)
- {
- int listIndex;
- for(listIndex = 0; listIndex < subsets[subsetIndex].index; listIndex++)
- {
- if(i == subsets[subsetIndex].list[listIndex])
- {
- return subsetIndex;
- }
- }
- }
- }
- // A function that does union of two sets of x and y
- // (uses union by rank)
- void Union(struct subset subsets[], int x, int y, int V)
- {
- int xroot = find(subsets, x, V);
- int yroot = find(subsets, y, V);
- // Attach smaller rank tree under root of high rank tree
- // (Union by Rank)
- if (subsets[xroot].index < subsets[yroot].index)
- {
- //subsets[xroot].parent = yroot;
- int index1;
- for(index1 = 0; index1 < subsets[xroot].index; index1++)
- {
- subsets[yroot].list[subsets[yroot].index++] = subsets[xroot].list[index1];
- }
- subsets[xroot].index = 0;
- }
- else
- {
- int index1;
- for(index1 = 0; index1 < subsets[yroot].index; index1++)
- {
- subsets[xroot].list[subsets[xroot].index++] = subsets[yroot].list[index1];
- }
- subsets[yroot].index = 0;
- }
- }
- // Compare two edges according to their weights.
- // Used in qsort() for sorting an array of edges
- int myComp(const void* a, const void* b)
- {
- struct Edge* a1 = (struct Edge*)a;
- struct Edge* b1 = (struct Edge*)b;
- return a1->weight > b1->weight;
- }
- // The main function to construct MST using Kruskal's algorithm
- void KruskalMST(struct Graph* graph)
- {
- int V = graph->V;
- int E = graph->E;
- struct Edge result[V]; // This will store the resultant MST
- int e1 = 0; // An index variable, used for result[]
- int i = 0; // An index variable, used for sorted edges
- // Step 1: Sort all the edges in non-decreasing order of their weight
- // If we are not allowed to change the given graph, we can create a copy of array of edges
- qsort(graph->edge, graph->E, sizeof(graph->edge[0]), myComp);
- // Allocate memory for creating V subsets
- struct subset *subsets = (struct subset*) malloc( V * sizeof(struct subset));
- // Create V subsets with single elements
- int e;
- int v = 0;
- int usedArray[V];
- int arrayIndex = 0;
- int subsetIndex = 0;
- for (e = 0; e < E; ++e)
- {
- struct Edge checkEdge = graph->edge[e];
- int sourceNum = checkEdge.src;
- int index;
- int flag = 0;
- //--------------- For source node---------------------------
- for(index = 0; index < arrayIndex; index++)
- {
- if(sourceNum == usedArray[index])
- {
- flag = 1;
- break;
- }
- }
- if(flag == 0)
- {
- usedArray[arrayIndex++] = sourceNum;
- subsets[subsetIndex].list = (int*) malloc(sizeof(int));
- subsets[subsetIndex].list[subsets[subsetIndex].index++] = sourceNum;
- subsetIndex++;
- }
- //----------------- For destination node---------------------
- flag = 0;
- int DesNum = checkEdge.dest;
- for(index = 0; index < arrayIndex; index++)
- {
- if(DesNum == usedArray[index])
- {
- flag = 1;
- break;
- }
- }
- if(flag == 0)
- {
- usedArray[arrayIndex++] = DesNum;
- subsets[subsetIndex].list = (int*) malloc(sizeof(int));
- subsets[subsetIndex].list[subsets[subsetIndex].index++] = DesNum;
- subsetIndex++;
- }
- }
- // Number of edges to be taken is equal to V-1
- while (e1 < V - 1)
- {
- // Step 2: Pick the smallest edge. And increment the index for next iteration
- struct Edge next_edge = graph->edge[i++];
- int x = find(subsets, next_edge.src, V);
- int y = find(subsets, next_edge.dest, V);
- // If including this edge does't cause cycle, include it
- // in result and increment the index of result for next edge
- if (x != y)
- {
- result[e1++] = next_edge;
- Union(subsets, next_edge.src, next_edge.dest, V);
- }
- // Else discard the next_edge
- }
- // print the contents of result[] to display the built MST
- printf("Following are the edges in the constructed MST\n");
- int sum = 0;
- for (i = 0; i < e1; ++i)
- {
- printf(" Edge :%d -> %d == %d\n", result[i].src, result[i].dest, result[i].weight);
- sum = sum + result[i].weight;
- }
- printf("\n ------> Minimum weight = %d\n",sum);
- return;
- }
- // Driver program to test above functions
- int main()
- {
- /* Let us create following weighted graph
- 10
- 20-------30
- | \ |
- 6| 5\ |15
- | \ |
- 70-------50
- 4 */
- int V = 4; // Number of vertices in graph
- int E = 5; // Number of edges in graph
- struct Graph* graph = createGraph(V, E);
- // add edge 0-1
- graph->edge[0].src = 20;
- graph->edge[0].dest = 30;
- graph->edge[0].weight = 10;
- // add edge 0-2
- graph->edge[1].src = 20;
- graph->edge[1].dest = 70;
- graph->edge[1].weight = 6;
- // add edge 0-3
- graph->edge[2].src = 20;
- graph->edge[2].dest = 50;
- graph->edge[2].weight = 5;
- // add edge 1-3
- graph->edge[3].src = 30;
- graph->edge[3].dest = 50;
- graph->edge[3].weight = 15;
- // add edge 2-3
- graph->edge[4].src = 70;
- graph->edge[4].dest = 50;
- graph->edge[4].weight = 4;
- KruskalMST(graph);
- return 0;
- }
// Output:
B: Prim's algorithm
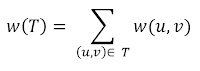




Không có nhận xét nào:
Đăng nhận xét